|
|
|
|
|
|
|
|
|
L'analyse de la transformation des valeurs en prix de production est développée
sous les contraintes de la reproduction élargie du capital.
A partir d'un système en valeur, il est
possible de calculer des prix de production qui sont égaux aux coûts
de production augmentés du profit.
Nous posons t = 1+ r
Sous forme matricielle classique le système
en prix de production est:
[ - W1 c1t
v1t
0 ] x1 = d1
[
0 c2t -W2
v2t 0
] x2 = d2
[ 0
c3t
v3 t
- W3 0 ] x3 = d3
[ 0 c4t
v4t -
W4 ] x4 = d4
Où di = - (Kfi r+ ai)
et, enfin, sous forme matricielle condensée : AX = D.
Dans ce système les inconnues sont :
A) les quatre coefficients de transformation xi,
B) les parts du capital total engagé affecté à chaque
branche.
Le taux de profit est défini par :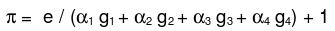
Le taux de profit a ici un statut particulier. Il est déterminé
par la répartition du capital et du travail entre les branches. Mais
pour chaque vecteur d'affectation du capital engagé, il constitue un
paramètre du système de détermination des prix de production
de marché (xi = f (taux de profit)).
La matrice A est une matrice paramétrée par t.
La résolution d'un tel système passe donc par trois
phases :
1. recherche de la répartition requise de la masse du capital social
disponible entre les différentes branches,
2. le calcul des coefficients de transformation,
3. vérification du respect de l'égalité du capital total
engagé exprimé en valeurs et en prix de production.
|
|

