|
|
|
|
|
|
|
|
|
|
L'analyse de la transformation des valeurs en prix de production est développée
sous les contraintes de la reproduction élargie du capital.
1. Le montant du capital social est supposé constant (nous poserons
par exemple, KT = 1 000 milliards d'euros).
2. La transformation des valeurs des marchandises en prix de production
suppose :
a ) le transfert de capitaux entre les branches,
b ) la satisfaction du besoin social,
c ) l'établissement d'un taux de profit moyen
égal à :
Taux de profit =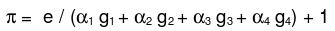
Le système en prix de production est construit à partir du
système en valeurs.
Dans chaque branche, les prix de production sont égaux aux coûts
de production augmentés du profit :
Branche I : (a1 + x2 c1+ x3 v1) + r (Kf1 + x2c1 + x3 v1)
= x1 W1
Branche II : (a2 + x2 c2+ x3 v2) + r (Kf2 + x2c2 + x 3v2) = x2
W2
Branche III : (a3 + x2 c3+ x3 v3) + r (Kf3 + x2c3 + x 3v3) = x3
W3
Branche IV : (a4 + x2 c4+ x3 v4) + r (Kf4 + x2c4 + x 3v4) = x4 W4
Dans ce système, les inconnues sont les quatre coefficients de transformation
xi.
L'établissement de prix de production, en substitution aux valeurs
des marchandises, modifie la structure de prix et tout changement dans la
structure des prix perturbe nécessairement l'équilibre existant.
Lorsqu'intervient une modification des prix, l'équilibre ne peut
être restauré que par un changement dans la répartition
du travail social. Et, en mode de production capitaliste, une nouvelle répartition
du travail passe nécessairement par une nouvelle répartition
du capital entre les branches.
De par notre hypothèse de constance du montant total du capital
engagé dans l'économie (1 000 milliards d'euros, par exemple),
nous avons :
1 000 = S Kfi + S ci + S vi = S Kfi + x2 S ci + x3 S vi
Le capital social est réparti entre toutes les branches, de façon
à ce que le montant du capital engagé évalué en
prix de production soit toujours égal à 1.000 milliards d'euros.
Les parts du capital engagé total dans chaque branche constituent
les quatre inconnues complémentaires.
Le taux de profit a ici un statut particulier. Il constitue un paramètre
du système de détermination des prix de production de marché,
lui même déterminé par la répartition du capital
et du travail entre les quatre branches. Ceci peut être montré
en isolant sur la gauche les variables, et sur la droite les éléments
constants ou paramétrés, une ligne « i » de ce système
peut être re-écrite sous la forme :
x2 ci + x2ci r - xi Wi + x3 vi r + x3 vi = - (Kfi r+ ai)
ou encore, si nous posons t = 1+ r :
Branche I : - W1 x1 + c1
t x2 + v1
t x 3 + 0 x4 = - (Kf1 r + a1)
Branche II : 0 x1 +
[c2 t - W2] x2 + v2
t x3 + 0 x4 = - (Kf2 r + a2)
Branche III : 0 x1 +
c3
x2 + [v3 t - W3 ] x3 + 0 x4 = - (Kf1 r +
a3)
Branche IV :
0 x1 +
c4
x2 +
v4
t x3 - W4 x4 = - (Kf1 r + a4)
Du point de vue du système de détermination des prix de production,
nous remarquons que les termes : - (Kfi r + ai) sont des paramètres
qui dépendent uniquement de la répartition du capital social
et des durées d'amortissement, éléments supposés
connus.
Aussi nous pouvons écrire di = - (Kfi r + ai) ou encore :
Branche I : - W1
c1t
v1
t 0 x1 = d1
Branche II : 0 [c2
t - W2] v2
t 0 x2 = d2
Branche III : 0
c3
t [v3 t - W3 ]
0 x3 = d3
Branche IV :
0
c4
t
v4
t - W4 x4 = d4
soit sous forme matricielle plus classique :
[ - W1 c1t
v1t
0 ] x1 = d1
[ 0 c2t -W2 v2t
0 ] x2 = d2
[ 0 c3t
v3t - W3 0
] x3 = d3
[ 0 c4t
v4 t - W4
] x4 = d4
et, enfin, sous forme matricielle condensée : AX = D.
La matrice A est une matrice paramétrée par t, dont le déterminant
doit être différent de zéro pour que le système
ait une solution acceptable différente de la solution triviale xi =
0.
Résoudre un tel système revient à déterminer
si la colonne D est une combinaison linéaire des colonnes de la matrice
A. Et si les di ne sont pas tous nuls le système est dit non homogène
et les équations doivent être indépendantes pour qu'une
solution unique puisse être trouvée. En effet, un tel système
est déterminé si, et seulement si, son déterminant
est différent de zéro. Il n'est donc pas possible de calculer
t selon la méthode usuelle mise en l'honneur par L. von Bortkiewicz.
Nous poserons donc l'hypothèse additionnelle que r est déterminé
par les conditions de production, c'est à dire dépend des compositions
organiques de chaque branche, de la répartition du capital entre celles-ci
et du taux d'exploitation (ce dernier est posé identique dans toutes
les branches) selon la formule présentée ci-dessus.
La résolution d'un tel système passe donc par trois
phases :
1. la recherche de la répartition requise de la masse du capital
social disponible entre les différentes branches,
2. le calcul des coefficients de transformation,
3. la vérification du respect de l'égalité du capital
total engagé exprimé en valeurs et en prix de production.
Suite |